inamerrata

The efficient market hypothesis — that prices in a market immediately adjust to fully reflect new information as soon as it becomes available — is probably the primary foundation of the success of markets at allocating resources: eg, making the prices people are willing to pay at supermarkets influence what farmers produce and how much oil gets drilled to power trucks and trains to transport food around the country or the world. What’s interesting is that despite the copious evidence that it works in practice — food does make it to supermarkets both more reliably and more cheaply using free markets than alternatives — it’s clearly not actually true: prices do get completely out of whack with “reality” and you get a bubble, which ends up forcing pretty painful corrections when the eventually burst. It seems like avoiding bubbles would be a win, but it’s not usually clear when they’re actually happening (after all, big price increases could actually be an accurate indication of reality, right up until a crash proves they weren’t), and in some sense it’s not really even clear why they happen in the first place.

I had a thought the other day that it might be interesting to simulate an asset market to test out an idea that I’d been pondering, to see if bubbles and crashes occurred or not. It didn’t take long to get a pretty serious price crash:

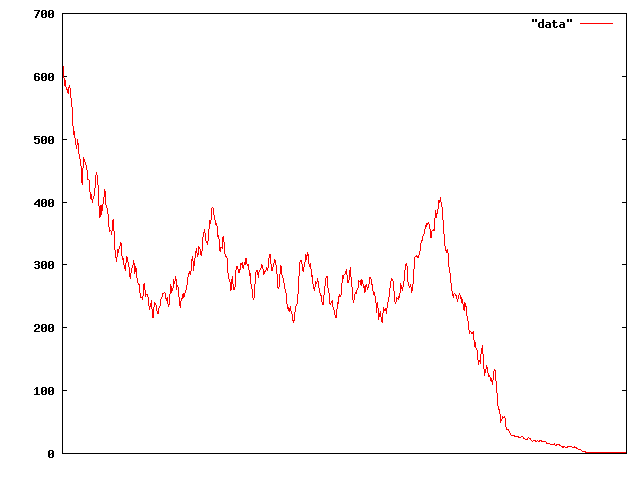But after the crash, things bounced back okay and stayed pretty stable:

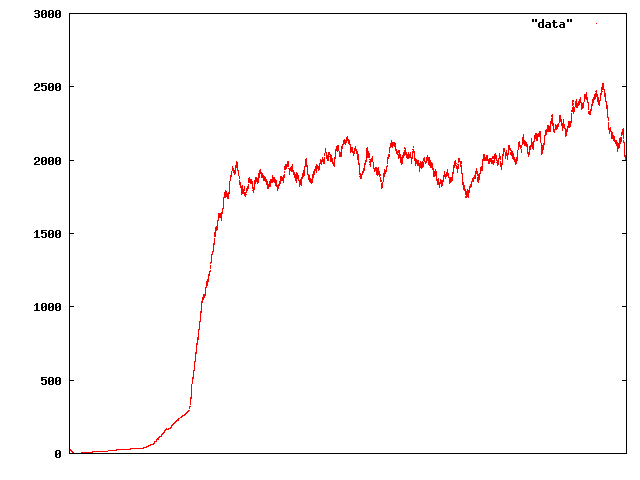That time series is twenty times as long as the first, so except for a bit of ups and downs, it looks like it might have actually stabilised at some sort of “fundamental” price. But sadly for our virtual traders, it turned out not:

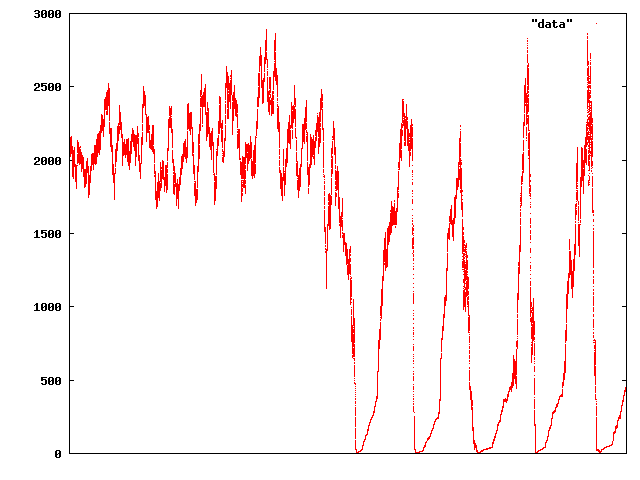That time period’s about six times as long as the previous, so about 120 times as long as the initial crash snapshot. And it’s not really a market that looks very pleasant to participate in either — and going on just a little further ends up with what appears to be a permanent price crash:

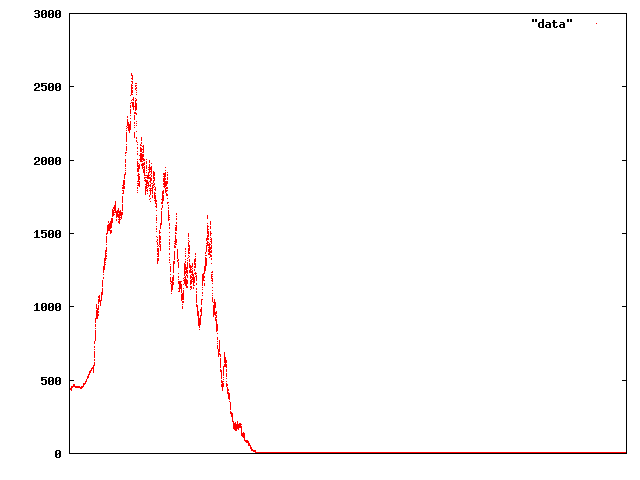The scale here is back to about the same as the initial recovery.

So what’s happening? As a pure simulation, all the behaviour here is implied by the initial setup. And that’s this: fifty simulated traders each start with $11,000, randomly choose an initial valuation for the assets available to trade, and based on that valuation purchase a number of those assets at $500 each. This is then followed by a series of rounds (the graphs above are from round 1 to 160,000), where each trader offers a buy and sell price for one asset. These prices are calculated by taking their current valuation for the assets, and adjusting it by two randomly calculated percentages r³, where r is between 1% and 51%, so they’re offering to buy for less than their valuation or sell for more than it. Those offers are collected, and if there’s any overlap (someone wants to buy for more than someone else wants to sell), a mid-point price is selected, and the trades are made at that price. If an individual trader is broke, their buy price is 0; if they don’t have any assets, their sell price is set to infinity.

Apart from the initial purchase, fundamentals have absolutely no influence on this market, or, more particularly the traders’ valuations of the worth of the assets being traded. There are no dividends, there’s no intrinsic worth to the assets, no monetary benefits or drawbacks to owning assets, no external influence after the initial setup, and it’s entirely zero-sum: any profits one trader makes come at an equal cost to some other trader.

So the traders try to out-interpret the market, by taking their previous estimated value and the price of the last trade, and extrapolating linearly. So if they thought it was worth $600, and the market thought it was worth $200 more at $800, they figure next round it will have another $200 increase and be worth $1000, and the same on the way down. If there weren’t any trades in the previous round, they’ll randomly change their valuation by between -5% and +5%. So when prices start going up, everyone keeps raising their prices for the next round, until nobody has enough money to buy anymore, and the prices reverse, until it’s down to just above zero, and then it’s back the other way. Medium-term stability only happens by good luck, long-term stability only happens when enough traders are broke that the ability of traders to randomly increase their valuations for even a few rounds in a row is heavily restricted.

Of course, that means every trader is explicitly refuting the efficient market hypothesis. If you do the opposite and assume it, ie have every trader immediately set their internal valuation to the market price, you get one round of trades setting a consensus price from trades based on each traders individual, private valuation, but then that’s it. No bubbles, no crashes, no periodic variation.

Which seems like it makes sense: if you’ve got a system that allows positive feedback loops on valuations, you’ll get prices rising or crashing; if the feedback’s limited and randomised, you’ll get both happening randomly. And “extrapolate the current trend” is definitely a positive feedback loop. I’d almost argue that all technical trading is positive-feedback: it assumes there are trends, then acts in ways that partially support the trend, and partially profit from the trend. If there’s an upward price trend, you buy, increasing demand, and supporting the upward price trend; if there’s a stabilising or downward price trend, you sell, dropping demand and supporting a downward price trend.

So I guess that’s my theory: bubbles and their corresponding crashes are a natural feature of markets that have a signficant number of technical traders, that is, traders who act based on their predictions of how other traders will act, rather than any inherent value they see in the things they’re trading. That might or mightn’t be an obvious conclusion. It seems kind-of obvious, but given the amount of purely technical advice in sharemarket books — teaching you not how to evaluate companies, so much as how you should expect the market to behave based on the same information everyone else has about how the market has been behaving; maybe it’s not.

If you could go a step further and say that the only profit technical investors can expect is from the losses of other technical investors, that could make things really interesting. I suspect something like it is close to true, if you can assert that your fundamental investors never individually make a loss. You can do that by assuming they have a personal, intrinsic valuation of the asset at $x, and will never buy one for more than that, or sell one for less than that, but that valuation is naturally going to change over time due to external factors (you become richer, so you’re willing to pay more for things; your priorities change and you value the asset more or less; the asset changes to become more or less useful/pleasing), and I don’t really see how to factor that in.